Solve the simultaneous equations y = 2x3 and x^2 y^2 = 2 Let the first equation be equation 1 and the second equation be equation 2 Firstly, you must substitute equation 1 into equation 2 This is because there are currently two unknown values in each equation (x and y) and therefore you must eliminate one of them so that you just have x's
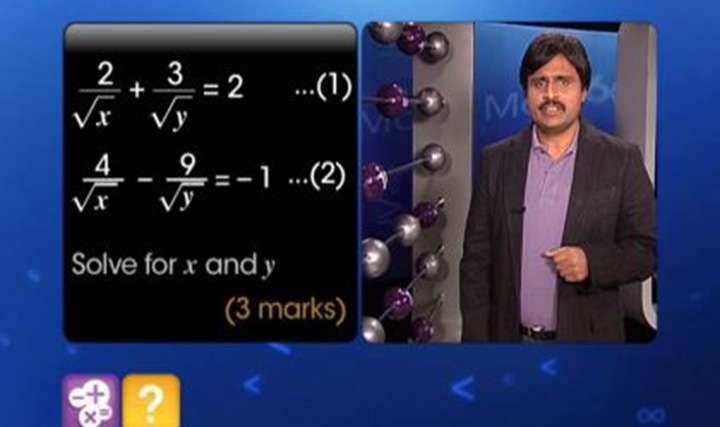
2/x-1+3/y+1=2 3/x-1+2/y+1=13/6- This DE has order 2 (the highest derivative appearing is the second derivative) and degree 1 (the power of the highest derivative is 1) b) `((dy)/(dx))^52x=3 sin(x)sin(y)` This DE has order 1 (the highest derivative appearing is the first derivative) and degree 5 (the power of the highest derivative is 5) c) `(y'')^42(y')^75y=3`8x2y2/4x3y3 Final result 2x5y5 Step by step solution Step 1 y2 Simplify —— 4 Equation at the end of step 1 y2 ( ( (8 • (x2)) • ——) • x3) • y3 4 Step 2 Equation at the end of step 2 y2 Finding limit of \frac {x^2y^2} {x^3y^3} as (x,y)\to (0,0) duplicate Finding limit of x3y3x2y2
2/x-1+3/y+1=2 3/x-1+2/y+1=13/6のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 | ||
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
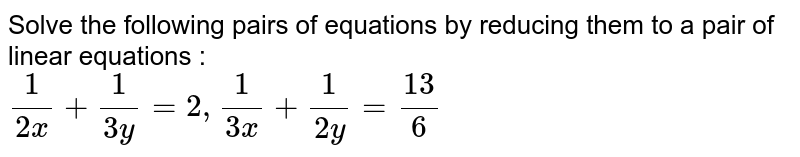 | 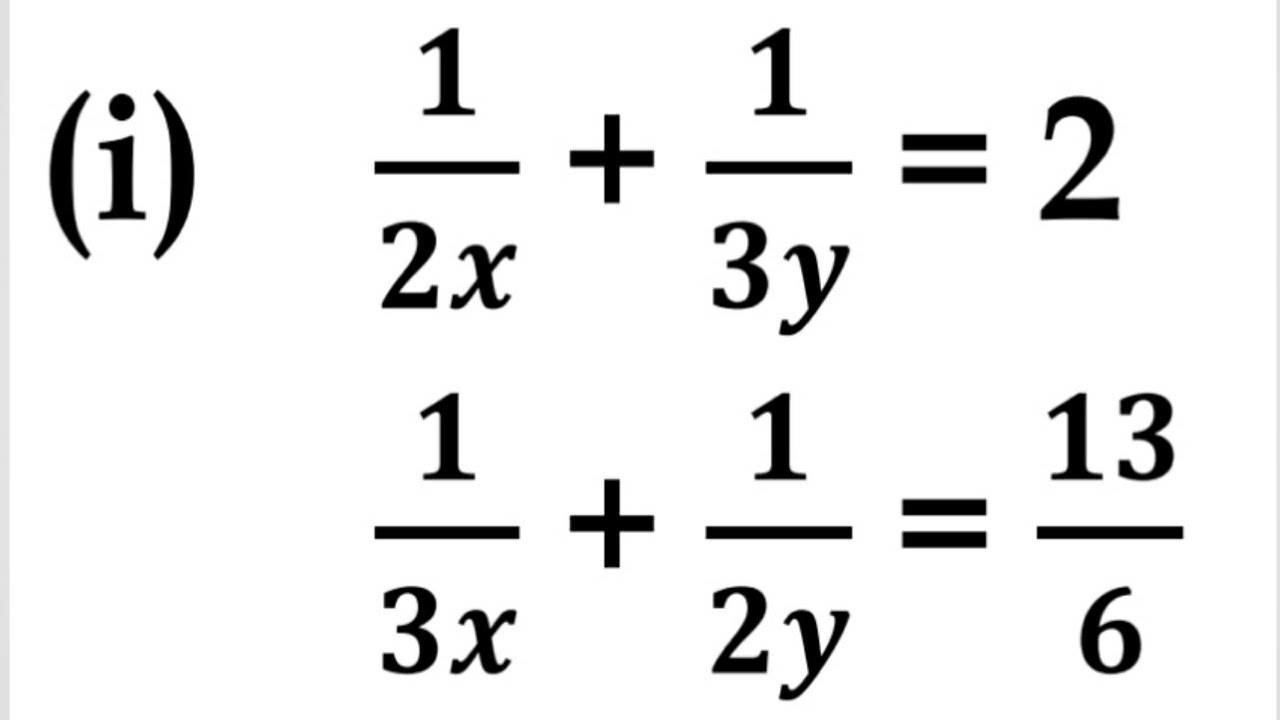 |  |
 |  |  |
 |  | |
 | ||
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 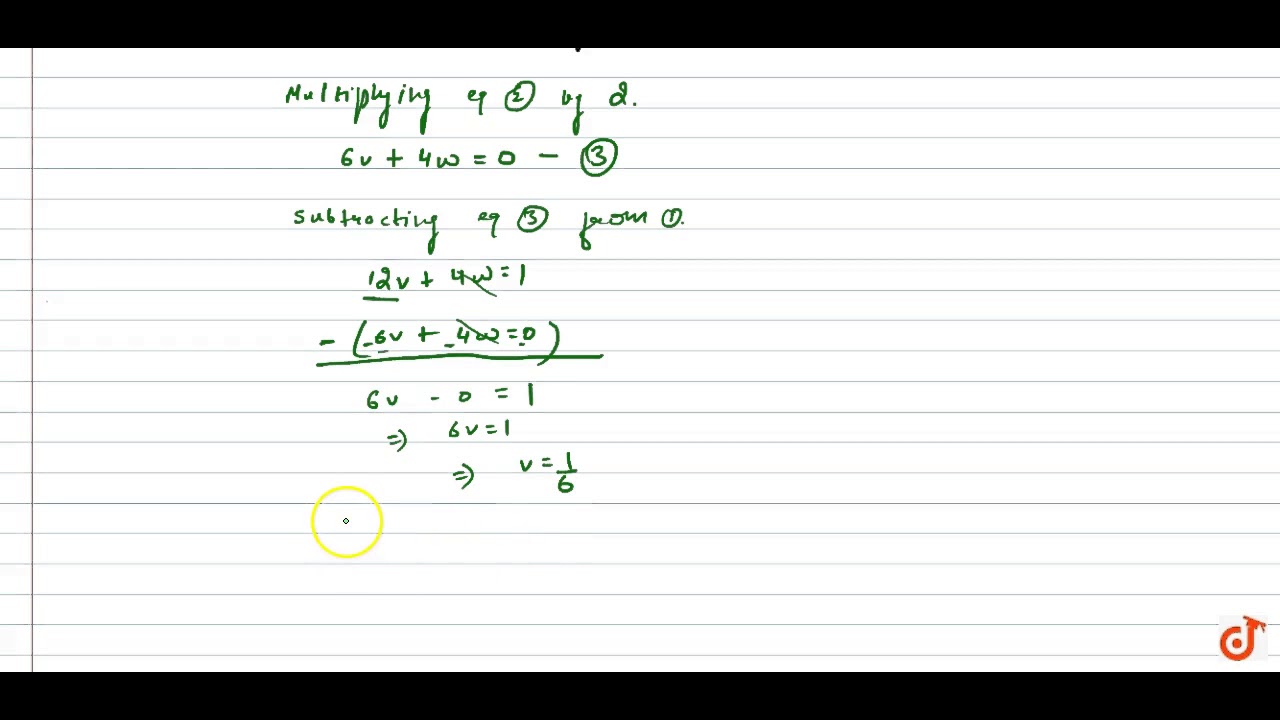 | |
 |  |  |
 | 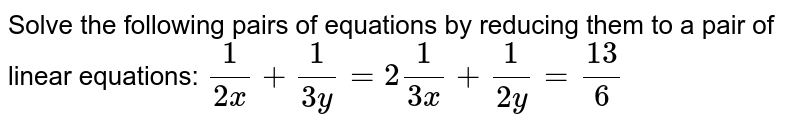 |  |
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
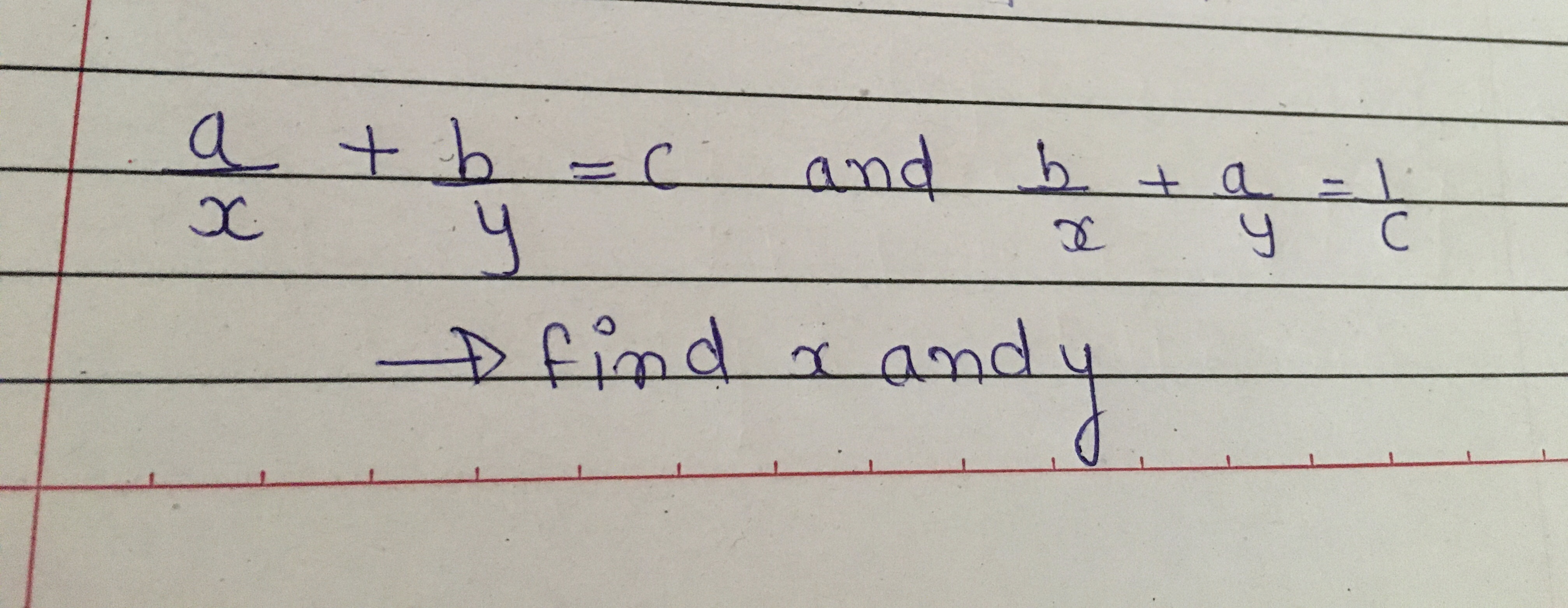 |  | |
 |  | |
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 | ||
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「2/x-1+3/y+1=2 3/x-1+2/y+1=13/6」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
For y = 0,1,2,3; Misc 16 Solve the system of the following equations 2/x 3/y 10/z = 4 4/x 6/y 5/z = 1 6/x 9/y /z = 2 The system of equations are 2/x 3/y 10/z = 4 4/x




